|
Hier findet ihr eine Anleitung des sogenannten 2-Look PLL der Fridrich Methode, das Vertauschen der Eck- und Kantensteine der letzten Ebene in 2 Schritten.
Für 2-Look PLL braucht man nur 7 (wenn man jeweils einen A- und einen U-Perm weglässt sogar nur 5) Algorithmen anstelle von 21.
Die Symbole stellen die oberste Ebene aus der Vogelperspektive dar.
Schritt 1:
Im 1. Schritt positioniert man alle Ecken richtig. Dazu stehen folgende Algorithmen zur Verfügung (Kanten ignorieren):
| ID | Symbol | Algorithmus |
PLL 01
A-Perm. | 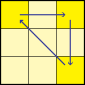 | Lw' U R' D2 R U' R' D2 R2, oder
y2 (L' B L') (F2 L B' L') (F2 L2), oder
R' U2 R2 U' L' U R' U' L U R' U2 R, oder
x R' U R' D2 R U' R' D2 R2, oder
y2 z F2 R U2 R' U2 F2 L' U2 L U2 |
PLL 02
A-Perm. | 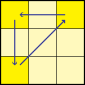 | Rw U' L D2 L' U L D2 L2, oder
y x R2 D2 R U R' D2 R U' R, oder
y R' U2 R U' L' U R U' L U R2 U2 R, oder
y' z U2 L' U2 L F2 U2 R U2 R' F2, oder
y2 z' F2 L' U2 L U2 F2 R U2 R' U2 |
PLL 03
E-Perm. | 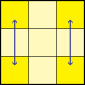 | x' R U' R' D R U R' Uw2 R' U R D R' U' R, oder
x' R U' R' D R U R' D2 L' U L D L' U' L, oder
z' R' F R2 U R' B' R U' R2 F' R z R B R', oder
y x U R' U' L U R U' r2' U' R U L U' R' U, oder
(r' R' U') (L D' L' U L) (R U' R' D R) U |
Schritt 2:
Im 2. Schritt werden die Kanten positioniert. Danach ist der Cube gelöst. Folgende Algorithmen braucht man dafür:
PLL 04
Z-Perm. | 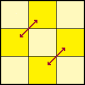 | M2 U M2 U M' U2 M2 U2 M' U2, oder
R2 U' R2 U R2 x' U2 R2 F U2 F' R2 U2, oder
R' U L' E2 L U' R L' U R' E2 R U' L', oder
U' l' U R U' D' R U D' R U' R' D2, oder
y F2 M2 F2 M2 U M2 U M2 U2 |
PLL 05
H-Perm. | 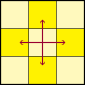 | M2 U M2 U2 M2 U M2, oder
R2' r2 U' L2 l2' U2 R2' r2 U' L2 l2', oder
F2 M2 F2 U' F2 M2 F2 U, oder
x U2 M2 U2 B' U2 M2 U2 B, oder
R U2 R' U' R' U' R2 U' R2 U2 R2 U2 R' U |
PLL 06
U-Perm. | 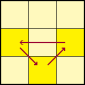 | R U' R U R U R U' R' U' R2, oder
M2 U M U2 M' U M2, oder
y2 M2 U M' U2 M U M2, oder
y' R2 U' y r U2 r' R U2 R' y' U R2 |
PLL 07
U-Perm. | 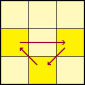 | R2 U R U R' U' R' U' R' U R', oder
M2 U' M U2 M' U' M2, oder
y2 M2 U' M' U2 M U' M2, oder
y2 R' U R' U' R' U' R' U R U R2, oder
y2 L' U' L U R U R' U2 L' U L U R U' R' |
DRUCKANSICHT
Impressum | Sitemap | Über Speedcube.de
|
|