

|
| |||||||||||||
|
||||||||
|
Hier findest du ein Tutorial zur Roux Methode von Gilles Roux, die zweitverbreiteste Speedcubingmethode für den 3x3x3 Cube (an dritter Stelle ist die Petrus Methode). Ich verwende Notations-Kürzel zum Angeben von bestimmten Positionen am Cube. UR steht z.B. für die Edgeposition zwischen der U-, und der R-Ebene. Außerdem solltest du die volle Notation beherrschen. Gilles Roux und Thomas Stadler entwickelten eine relativ außergewöhnliche Methode, den Rubik´s Cube zu Lösen. Bei dieser Methode werden zuerst zwei 3x2x1-Blöcke nebeneinander gebaut, dann die Ecken der oberen Ebene gelöst und zum Schluss die restlichen Edges in Position gebracht. Schritte:
Ich habe mir für die Roux Methode eine Start-Farbe ausgesucht, mit der ich immer anfange. Bei dieser Methode muss man also nicht Colour-Neutral sein. Man wird sogar (meinen Erfahrungen nach) schneller, wenn man eine feste Startfarbe hat. Meine Startfarbe ist weiß. Außerdem sollte man für die Roux Methode folgendes wissen: Rot ist gegenüber von Orange, Blau ist gegenüber von Grün und Weiß ist gegenüber von Gelb. Die 2 3x2x1 BlöckeEs werden (wie schon gesagt) 2 3x2x1 Blöcke (unten ausgerichtet) auf L und R gebaut (weiß unten). Dieser Schritt sollte (nach der Zeit, aber unbedingt) intuitiv gemacht werden, aber ich werde trotzdem eine Methode erklären:
Nun könnte dein Cube so in etwa aussehen:  Ecken lösenIn diesem Schritt werden die übrigen 4 Ecken gelöst. Also quasi folgendes: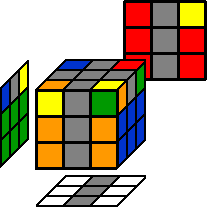 → Lösen → → Lösen → 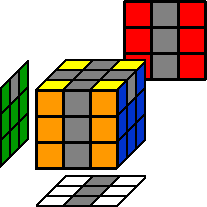
Besonders wichtig ist der Satz "Falls nötig musst du vorher und/oder nachher noch U, U' oder U2 ausführen" beim beiden Unterschritten, denn ansonsten weißt du nicht, welchen Algorithmen du anwenden musst. restliche Edges richtig kippen (auf "WeGe") und die Edges UL und UR lösenDie 6 restlichen Edges müssen nun richtig gekippt werden und die Edges an Position UL und UR richtig eingefüllt werden. In diesem Schritt werden die gegenüberliegenden Farben oben/unten nun gleichgesetzt. Bei mir z.B. Gelb und Weiß. Nennen wir diese Farben WeGe, OrRo und GrüBl.Die Blöcke müssen für diesen Schritt unten ausgerichtet links und rechts sein, damit M und U frei beweglich sind. Ziel ist es, die obere Fläche WeGe zu kriegen. Dazu dreht man die obere Ebene einfach so, dass eines der folgenden Muster zu sehen ist (grau = rot, grün, orange oder blau) und führt M' U M' aus:  | |
 | |
 | |
 | |
 oder oder
 Und nun musst du intuitiv die Positionen UL und UR mit den richtigen Edges befüllen (in meinem Fall gelb/grün und gelb/blau). Aber dazu darfst du nur die obere Ebene (U) und die mittlere Ebene (M) drehen. M2 darfst du immer drehen, M oder M' aber nur, wenn du danach U2 und danach wieder M oder M' drehst. Wenn du etwas falsches drehst, dann sind die Edges nichtmehr richtig gekippt. Probier am besten solange rum, bis du deine eigenen kleinen Algorithmen gefunden hast. Ich benutze z.B. M' U2 M um die Edge UB nach UF und die Edge DF nach UB zu transportieren. Das muss man sich einfach selbst beibringen. restliche Edges der M-Ebene vertauschenErstmal drehst du mit M, M' oder M2 die Centers richtig. Um die restlichen Edges der M-Ebene nun zu sortieren, braucht man nur 4 leichte Algorithmen:
Ich hoffe das Tutorial hat geholfen, wenn du Fragen hast oder denkst einen Fehler gefunden zu haben, dann schick bitte eine E-mail an webmaster@speedcube.de oder melde dich in unserem Speedcubing Forum! Tutorial by Aaron Mondal, Forums-Benutzername: Sidmoon; mit Freuden angepasst und eingestellt vom Webmaster Felk |
||||||||||